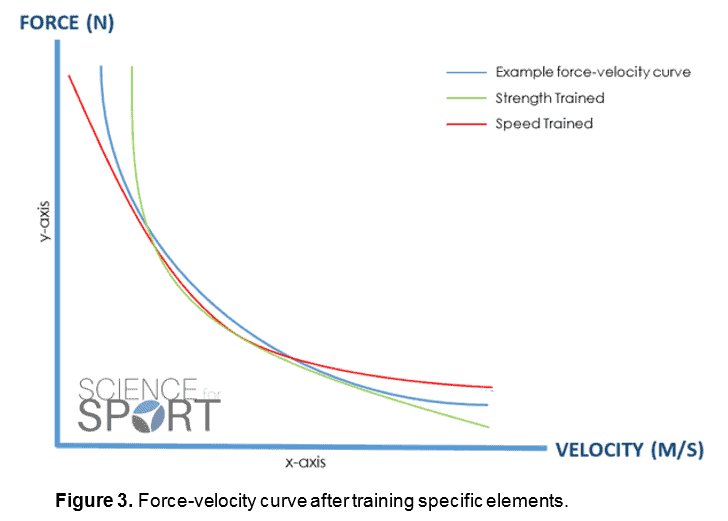
Tuossa kuvaajassa taitaa olla seuraavasti:
- Y -akseli on paino, joka on laskettu isometrisestä maksimista (tai voima mikä voidaan tuottaa isometrisestä maksimista)
- X -akseli on se muutos, mitä lihastyöllä saadaan tehtyä, eli kunka paljon saadaan kappaleen vauhtia kiihdytettyä tai jarrutettua.
a) Tällöin kiihtyvyyden 0 kohdassa ollaan isometrisessa maksimissa, jolloin lihas supistuu ja sen pituus pysyy saman.
b) Kun painoa vähennetään, niin siirrytään konsentrisen lihastyön puolelle ja lihas supistuu ja lyhenee, jolloin kappaleen kiihtyvyys on positiivinen.
c) Kun painoa lisätään, niin kappaleen kiihtyvyys on negatiivinen ja lihas supistuu ja venyy ja tuottaa voimaa konsentrisesti.
Siinä kohdassa, kun käyrä muuttuu x – akselin suuntaiseksi eksentrisen voimantuoton puolella, ollaan saavutettu tilanne, ettei lihaksilla voida enää jarrutta liikettä.
Tuossa kuvaajassa termit on vähän hankalasti, mutta voidaan ajatella, että y-akseli nostettava paino ja x -akseli se kiihtyvyys, mikä tuolle painolla saadaan.
Eri tieteissä käytetään termejä vähän eri lailla ja monesti tieteen sisällä määritellään erikseen se, mitä termit tarkoittaa. Näin tehdään monesti myös artikkeleiden alussa.
Kannattaa myös muistaa, että tuo käyrä on normalisoitu keskiarvo, jonka muoto muuttuu paljon eri henkilöiden välillä. Henkilö, joka on keskittynyt konsentriseen nopeusvoimaan käyrä menee aivan eri tavalla kuin henkilön, joka on keskittynyt eksentrisen voiman kehittämiseen. Käyrien perusmuoto on kuitenkin hyvin samanlainen.
Jos tuota mietitään vaikka painon ylös nostamisen kantilta, niin tuo tarkoittaa seuraavaa.
- Isometrisessä maksimissa, niin kappale pysyy paikallaan ja kumoaa maan vetovoiman.
- Konsentrisen voiman puolella, paino alle maksimin, niin kappaleen nousee kiihtyvällä vauhdilla ja kiihtyvyydelle ei ole muuta ylärajaa, kuin lihaksen supistusnopeus.
- Eksentrisen voiman puolella, niin lihaksen tuottama voima kumoaa painovoiman ja kappale putoaa hitaammin.
-- Kun painoa lisätään riittävästi, niin lihas ei pysty tuottamaan enempää voimaa, vaan se putoaa samalla vauhdilla oli painoa kuinka paljon tahansa.
-- Lihaksen eksentriseksi maksimiksi voidaan myös miettiä kohtaa, jossa lihas repää/hajoaa jne.