Biomekaniikka + fysiikka ja niiden variaatiot

[Pappi]

voima

voimantuotto

Edelleenkin, tuntuu siltä että ajattelet nyt jotenkin väärin.

Ei voimantuotto kasva, jos painoa lisätään vähitellen vaikka tuhanteen kiloon. Se paino kasvaa tuhanteen kiloon, ja samalla menee lujempaa alas.

 

[jassoo7]

Minun käsittääkseni tuo menisi suunnilleen näin:

Isometrinen, tuo keskipiste. Pidät painoa hauiskäännössä puolessavälissä. Et saa sitä ylös, mutta ei se alaskaan mene. Jännität vaan täysillä ja saat pidettyä sen siinä.

Eksentrinen.....Joku alkaa latoa tankoon lisää painoa. Tangon nopeus kasvaa alas sitä mukaa kun paino kasvaa. Et jaksa pitää sitä enää ylhäällä.

Vielä en tuuleta ja anna tunnustusta MUTTA mitä tapahtuu mikäli kukaan ei lado tuohon isometriseen lisää painoa? Ja jossain vaiheessa tulee väsy! Mitä lihas tekee? Suunta on kyllä eksentrinen mutta lihas tuottaa? enemmän vai vähemmän voimaa?

 

[jassoo7]

Edelleenkin, tuntuu siltä että ajattelet nyt jotenkin väärin.

Ei voimantuotto kasva, jos painoa lisätään vähitellen vaikka tuhanteen kiloon. Se paino kasvaa tuhanteen kiloon, ja samalla menee lujempaa alas.

Sekoitat minun sanat mitä tutkijat sanoo.

Mutta tuo loppu puhutko tuossa boldatussa tekstissä eksentrisestä suunnasta?

Tutkimuksissa sanotaan että tilanteesta riippumatta eksentrisesti tuotetaan enemmän voimaa mitä konsentrisesti.

 

[Pappi]

tuotetaan enemmän voimaa

Ei siinä mitään tuoteta. Se "voima" on siis se painon määrä. Lisätään painoa, "voimaa", ja se menee lujempaa alas.

Lihasvoima siis ei tietenkään lisäänny jumalaisiin lukemiin, jos painoa laitetaan miljoona kiloa.

 

[En kerro!!!]

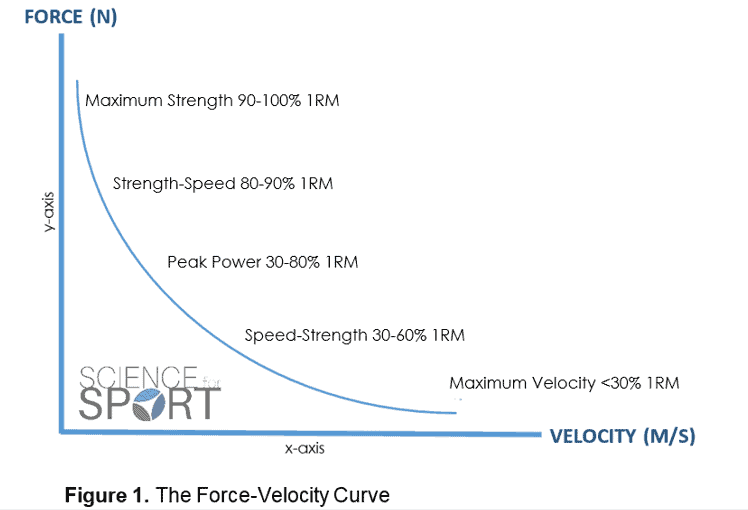
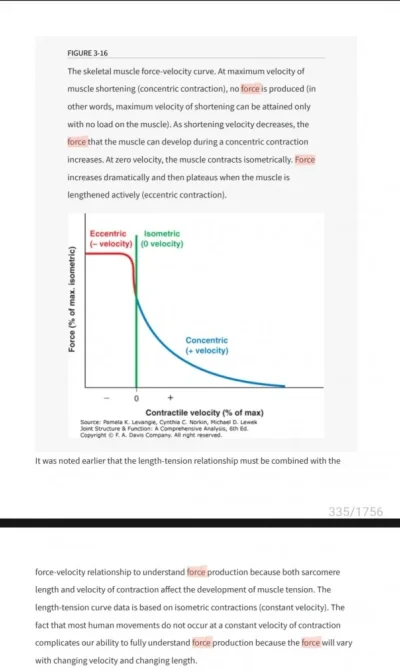
Aa joo meni ohi! reilulla marginaalilla +/- 10-15kg 150kg ympärillä. Mutta kuten jo totesin yhtälössä on niin montaa muuttujaa joita ei voida vakioida että laski tuon sitten miten tahansa niin aina menee jotenkin metsään.

No niin, lasketaan esimerkiksi sen mukaan, että voitaisiin tehdä negatiivinen vaihe, täysillä jarruttaen kolmessa sekunnissa 150 kilolla ja penkkimaksimi olisi tuon 100 kg. Maksiminoston kestäessä 5 sekuntia. Oletetaan yksinkertaistuksena, että sekä nosto-, että laskuvaiheessa liike on tasaisesti kiihtyvää. Noston alussa, sekä negatiivisen toiston alussa tangon nopeus on 0.

Konsentrinen vaihe:
Massa (m) = 100 kg
Nostoaika (t) = 5 s
Kiihtyvyys (a)
Matka (s) = 0,5*a*t^2 = 0,5 m
-> a = 2s/t2 = 2*0,5 m / (5 s)^2 = 1/25*m/s^2 = 0,04 m/s^2.
Maan vetovoima kiskoo myös tankoa alaspäin koko ajan, joten nostaja joutuu kohdistamaan tankoon voiman F = m*(g+a) = 100 kg*(9,81+0,04)m/s^2 = 985 N.

Eksentrinen vaihe:
Matka ja maan vetovoima ovat samat, kuin konsentrisessa vaiheessa.
m = 150 kg
t = 3 s
-> a = 2*0,5 m / (3 s)^2 = 0,111... m/s^2
Nostajan tankoon kohdistama voima F = 150 kg*(9,81-0,111...)m/s^2 = 1455 N.

Eksentrisessä vaiheessa siis voimaa joudutaan tuottamaan 1,477 kertaa enemmän. Arviosi mukaan noin +- 10%.
Eli arvioit, että eksentrisessä vaiheessa voimaa voidaan tuottaa n. 38-58% enemmän, kuin konsentrisessa vaiheessa.
Mutta kuitenkin olit sitä mieltä, ettei eksentrisessä vaiheessa ole mahdollista tuottaa enempää voimaa.

 

[Pappi]

Näin tarkemmin ajateltuna, suottaapi olla, että olen itsekkin pihalla kuin lumiukko aiheesta

Hyvää yötä, MinEn jaksa

 

[Force]

Nuo laittamasi graafit näyttää juuri sen mitä nopeampaa eksentrinen liike on sitä enemmän voimaa tuotetaan ja taas mitä nopeampaa konsentrinen liike on sitä vähemmän voimaa tuotetaan. Eikö?

Niin. Miksi muuten jos on tollanen kuva missä lukee 1+1 = 2. Niin pitää kysyä että lukeeko tossa kuvassa 1+1 = 2 ?

 

[jassoo7]

Ei siinä mitään tuoteta. Se "voima" on siis se painon määrä. Lisätään painoa, "voimaa", ja se menee lujempaa alas.

Lihasvoima siis ei tietenkään lisäänny jumalaisiin lukemiin, jos painoa laitetaan miljoona kiloa.

Eli ollaan isometrisessä tilassa.

Se vastus yrittää tuottaa rotaatiota sinun kyynärniveleen eksentriseen suuntaan siitä puhutaan termillä "tuottaa voima" (ihmis liike on liikettä akselipisteiden ELI nivelten ympärillä. Mekaniikassa ja biomekaniikassa puhutaan vääntömomentista tai lontooksi torque. Kun otat painon käteen ja alat liikuttaa sitä lihasvoimalla nivelessä tuotetaan kiertyvää liikettä. Toiseen suuntaan sitä sinun antamassa esimerkissä liikuttaa lihas ja toiseen suuntaan kädessä oleva paino tai tanko jota nimitetään vastukseksi. Molemmat sekä lihas että paino VOIVAT saada nivelessä liikettä aikaiseksi riippuen nivelen kulmasta ja voiman määrästä. Nopea yhteenveto tästä varmaankin tuttua mutta varuiksi kertasin. )

Okei jatketaan nyt lihaksesi ei jaksa olemassa olevalla kuormalla enää pitää isometrista tilaa ja liike kääntyy eksentriseksi. (Ilman olemassaolevaan vastukseen lisättyä kuormaa) kysymys: tuotatko lihaksella konsentrisesti tällöin enemmän vai vähemmän voimaa?

 

[jassoo7]

Näin tarkemmin ajateltuna, suottaapi olla, että olen itsekkin pihalla kuin lumiukko aiheesta

Hyvää yötä, MinEn jaksa

Nuku mutta et ole pihalla!!!!!!!

 

[jassoo7]

Niin. Miksi muuten jos on tollanen kuva missä lukee 1+1 = 2. Niin pitää kysyä että lukeeko tossa kuvassa 1+1 = 2 ?

Että mitä että?

 

[jassoo7]

Eli arvioit, että eksentrisessä vaiheessa voimaa voidaan tuottaa n. 38-58% enemmän, kuin konsentrisessa vaiheessa.
Mutta kuitenkin olit sitä mieltä, ettei eksentrisessä vaiheessa ole mahdollista tuottaa enempää voimaa

Kumpaanko suuntaan sinä lihasta supistat? Mihinkä suuntaan se tuottaa voimaa VAIKKA vastus tuottaakin enemmän voimaa mutta se lihas maksimaalisesti edelleen tuottaa voimaa konsentrisesti. Se yrittää supistua! Se Ei venyessään tuota enemmän voimaa vaan vähemmän. Jos se tuottaa enemmän voimaa tanko joko pysähtyy tai nousee takaisin ylös!

Nyt käyn minäkin unille jatketaan huomenna.

 

[En kerro!!!]

Kumpaanko suuntaan sinä lihasta supistat? Mihinkä suuntaan se tuottaa voimaa VAIKKA vastus tuottaakin enemmän voimaa mutta se lihas maksimaalisesti edelleen tuottaa voimaa konsentrisesti. Se yrittää supistua! Se Ei venyessään tuota enemmän voimaa vaan vähemmän. Jos se tuottaa enemmän voimaa tanko joko pysähtyy tai nousee takaisin ylös!

Nyt käyn minäkin unille jatketaan huomenna.

Ei tuo kenellekään ole epäselvää, että lihas pyrkii supistumaan. Itse kuitenkin arvioit lihaksen pystyvän venyessään reilusti suurempaan voimantuottoon.

Jos nyt otetaan tuo ehdottamasi 150 kg paino negatiiviseen toistoon, niin 3 sekuntia kestävässä laskuvaiheessa joudut työntämään 148,3 kg:n voimalla. Eikö tämä ole aika paljon enemmän, kuin nostovaiheessa 100 kg tankoon kohdistuva voima? Riiteletkö nyt itsesi kanssa?

Jos taas sama paino nostetaan ja lasketaan tasaisella kiihtyvyydellä, siinä tapauksessa eksentrisessä vaiheessa tietysti tuotetaan vähemmän voimaa. Sijoita vaikka se 100 kg tuohon eksentrisen vaiheen yhtälöön ja valitse mieluinen kestoaika negatiiviselle toistolle.

 

[Force]

Okei. Mistä sitä kuormaa yleensä tuohon maksimaalisen konsentrisen voimantuoton päälle sitten ilmestyy?

Ja kysyisin sinulta myös että jos kerta tuo 0 piste (isometrinen) oli konsentrisen voimantuoton maksimi (105kg) niin mistä graafin isometrisen jälkeen tuleva konsentrinen osuus tulee tai miksi se on piirretty siihen koska luomassasi esimerkissäsi sitä ei voi ihmiskehossa olla tai tuottaa (105kg oli konsentrinen maksimi puolessa välissä liikettä). Voimaa aletaan siis tuottamaan kehon ulkopuoleltako esim avustajien toimesta vai mistä? Että konsentrisen voimantuoton jatkumo olisi graafissa järkevää esittää.

Mitä tällainen on? Miksi joku ihminen kirjoittaa tuollaista tekstiä ja kysyy tuollaisia. Huvikseni kirjoitan.

Mistä kuormaa ilmestyy? No käsillä laitetaan vaikka levyjä tankoon tai vetokumeja tai joku roikkuu tangossa tai jotain.

Tuo loppu meni ihan pitkin vittua. Kuvaaja ottaa kantaa siihen paljonko voimaa eri liikenopeuksilla pystyy saada aikaan. Ei se niiku mitenkään kuvaa että isometrisellä maksikuormalla tehtäisiin kokonainen toisto, ei riitä aivot ymmärtämään mistä tollainen ajatus.

Helpointa ymmärtää että käyrän oikeassa laidassa on kevyt kuorma ja kasvaa vasemmalle mentäessä. Oikealla ilman lisäpainoa kyykkyhyppy ja vasemmalla reilusti yli maksimin rauta.

Sama käyrä pelkästään konsentrisella puolella

 

[Force]

Kumpaanko suuntaan sinä lihasta supistat? Mihinkä suuntaan se tuottaa voimaa VAIKKA vastus tuottaakin enemmän voimaa mutta se lihas maksimaalisesti edelleen tuottaa voimaa konsentrisesti. Se yrittää supistua! Se Ei venyessään tuota enemmän voimaa vaan vähemmän. Jos se tuottaa enemmän voimaa tanko joko pysähtyy tai nousee takaisin ylös!

Nyt käyn minäkin unille jatketaan huomenna.

Ei jeesus sentään

Sillon kun lihas pitenee niin puhutaan että se tuottaa voimaa eksentrisesti, ei konsentrisesti. Se supistuu kuten lihas tekee ja tuottaa voimaa eksentrisesti pidentyessään. Tuon selvemmin sitä ei voi sanoa ja olen varma että et tajunnut.

Noissa käyrissä käsitellään lihaksen potentiaalia tuottaa voimaa eri nopeuksilla eli käytännössä eri kuormilla. Ei noita käyriä voi yrittää käyttää yksittäisen tietyllä painolla tehdyn toiston simulointiin.

 

[jassoo7]

Ei tuo kenellekään ole epäselvää, että lihas pyrkii supistumaan. Itse kuitenkin arvioit lihaksen pystyvän venyessään reilusti suurempaan voimantuottoon.

Jos nyt otetaan tuo ehdottamasi 150 kg paino negatiiviseen toistoon, niin 3 sekuntia kestävässä laskuvaiheessa joudut työntämään 148,3 kg:n voimalla. Eikö tämä ole aika paljon enemmän, kuin nostovaiheessa 100 kg tankoon kohdistuva voima? Riiteletkö nyt itsesi kanssa?

Jos taas sama paino nostetaan ja lasketaan tasaisella kiihtyvyydellä, siinä tapauksessa eksentrisessä vaiheessa tietysti tuotetaan vähemmän voimaa. Sijoita vaikka se 100 kg tuohon eksentrisen vaiheen yhtälöön ja valitse mieluinen kestoaika negatiiviselle toistolle.

No tottakai koska esimerkissäsi oli annettu arvot, liikesuunta (ehkä jopa tietoisesti näin päin esimerkin halutun lopputuloksen kannalta?) ja ymmärränkö oikein että olisit halunnut että olisin laskenut väärin esimerkkisi parametreilla?

Sitten lasku esimerkissä muutetaan aikaa, liikesuuntaa ja sille ajalle halutaan ratkaista uusi kuorma jolla aika määre saavutetaan tämä tottakai muuttaa yhtälön lopputulosta.

Myös hauska että loit myös esimerkin niin että lähdettiin penkkiä tekemään ala asennosta! No jos haluat että esimerkkisi olisi vertailu kelpoiset tulisi ne suorittaa samalla tavalla? Eikö? Eli ala asennossa 150kg tankoon. Kuten tuossa yllä mainitsin tulokseen ei vaikuta pelkkä voimien suuruus ero vaan kehossa liikkeen tuottamiseksi lihakset supistumalla saa aikaan vääntöä. (T= fma.) Eli kyllä nyt on ratkaistu 2 eri kuormalla voimat mutta yhtälöstä puuttuu vielä momentin varret. Penkissä ala asennossa nämä voidaan sanoa olevan suurimmillaan. Voimantuoton näkökulmasta rintalihaksen momentinvarsi akselipisteeseen nähden on pienimmillään. Sinä laskit tasaisella voimantuotolla ja vastuksen voiman määrällä mitä ei ikinä kehossa tapahdu.

Montako kertaa sinä penkki kisoissa tai kun treenaat esim saman noston aikana ensin lasket tangossa 150kg rinnalle avustajat repii painot pois ja työnnät sitten 100kg? Epäilen että et kovinkaan usein toki varmaan joku tekee mutta ei kovin moni.

 

[jassoo7]

Esimerkki @Force ja @En kerro!!! Istuvat auton kyydissä moottori pyörii. Force ajaa. En kerro haluaa päästä rehvakkaasti vauhtiin. Tässä vaiheessa molemmat katsovat voima nopeus käyrää ja toteavat että kyllä nopeampi kiihtyvyys konsentriseen suuntaan liene autolla eteenpäin? Vaatii voimantuollisesti vain vähän voimaa että saadaan nopea kiihtyvyys. Hyvä force painaa kaasua ja auto kiihtyy menikö kaikki sittenkään kuten graafissa olis esitetty? Sitten välähtää. Peruuttamalla auto kulkee 20-50% kovempaa ja/ tai tuottaa enemmän voimaa. Humoristinen esimerkki sori mutta mitenkä soveltuu taas siihen f=ma. No ei valitettavasti mitenkään. Jos parametrejä ei muuteta!

 

[jassoo7]

Nooo mitä sanoo oppikirja Joint struction & function 6 edition?

 

[En kerro!!!]

No tottakai koska esimerkissäsi oli annettu arvot, liikesuunta (ehkä jopa tietoisesti näin päin esimerkin halutun lopputuloksen kannalta?) ja ymmärränkö oikein että olisit halunnut että olisin laskenut väärin esimerkkisi parametreilla?

Sitten lasku esimerkissä muutetaan aikaa, liikesuuntaa ja sille ajalle halutaan ratkaista uusi kuorma jolla aika määre saavutetaan tämä tottakai muuttaa yhtälön lopputulosta.

Myös hauska että loit myös esimerkin niin että lähdettiin penkkiä tekemään ala asennosta! No jos haluat että esimerkkisi olisi vertailu kelpoiset tulisi ne suorittaa samalla tavalla? Eikö? Eli ala asennossa 150kg tankoon. Kuten tuossa yllä mainitsin tulokseen ei vaikuta pelkkä voimien suuruus ero vaan kehossa liikkeen tuottamiseksi lihakset supistumalla saa aikaan vääntöä. (T= fma.) Eli kyllä nyt on ratkaistu 2 eri kuormalla voimat mutta yhtälöstä puuttuu vielä momentin varret. Penkissä ala asennossa nämä voidaan sanoa olevan suurimmillaan. Voimantuoton näkökulmasta rintalihaksen momentinvarsi akselipisteeseen nähden on pienimmillään. Sinä laskit tasaisella voimantuotolla ja vastuksen voiman määrällä mitä ei ikinä kehossa tapahdu.

Montako kertaa sinä penkki kisoissa tai kun treenaat esim saman noston aikana ensin lasket tangossa 150kg rinnalle avustajat repii painot pois ja työnnät sitten 100kg? Epäilen että et kovinkaan usein toki varmaan joku tekee mutta ei kovin moni.

Kyse oli sinun omasta arviosta. Vaikuttaa siltä, että tajuat, että eksentrisessä vaiheessa voidaan tuottaa enemmän voimaa, mutta et ole vaan tajunnut ymmärtäneesi.

Ei sen penkkimaksimin tarvitse lähteä ala-asennosta, mutta konsentrisen vaiheen voimantuoton kannalta sillä ei ole merkitystä, onko tanko pysäytetty rinnalle, vai alkaako suoritus konsentrisella vaiheella.

Ja mitä järkeä olisi laittaa esimerkin henkilölle ala-asennossa 150 kg tankoon? Kyse on edelleen siitä 100 kg penkkipunnertajasta, joten tanko ei liikahtaisikaan. Mutta edelleen tuo sama henkilö kykenee arviosi mukaan laskemaan tuon 150 kg rinnalle siten, että eksentrinen vaihe kestää 3 sekuntia. Ja jos sinulle ongelma on siinä, että eksentrisen ja konsentrisen vaiheen suoritusajat ovat erit, voidaan sopia, että laskuvaihe kestää myös 5 s. Tässä tapauksessa tietysti vaaditaan entistäkin suurempaa voimantuottoa.

Ja mitä ihmettä tarkoitat sillä, että lasku_esimerkissä vaihdetaan liikesuuntaa? Tottakai liikesuunta on eri. Ei tankoa voi laskea ylöspäin.

Ihan sama kuinka monta muuttujaa lisäät yhtälöön (momenttivarret, voimantuotto eri nivelkulmilla/lihaspituuksilla ym.), lopputulos on aina sama. Eksentrissä vaiheessa on mahdollista tuottaa enemmän voimaa, kuin konsentrisessa.

Ja vielä selvennyksenä, jos 100 kg penkkipunnertaja laskee 100 kg rinnalle ja nostaa sen jälkeen ylös, tässä suorituksessa konsentrisen vaiheen voimantuotto oli suurempaa, kuin eksentrisen. Nostajalla olisi tietysti mahdollisuus tuottaa eksentrisessä vaiheessa enemmän voimaa, jolloin tangon liike hidastuu ja vaikka pysähtyy kesken laskun. Nostaja voi myös mahdollisesti tästä stoppikohdasta nostaa tangon ylös, mutta tämä ei edelleenkään tarkoita sitä etteikö nostajalla olisi mahdollista hallita negatiivisessa vaiheessa suurempiakin kuormia. Selkeästi suuremman kuorman pysäyttäminen, eikä varsinkaan nosto pysäytyskohdasta onnistu.

 

[jassoo7]

Kyse oli sinun omasta arviosta. Vaikuttaa siltä, että tajuat, että eksentrisessä vaiheessa voidaan tuottaa enemmän voimaa, mutta et ole vaan tajunnut ymmärtäneesi.

Eli olisit halunnut että lasken sen sinun antamilla parametreilla väärin. Jos olisin sanonut että noston uupumuksesta johtuen 100kg laskee sen 3 sek olisit sanonut että en osaa laskea.

Ja mitä järkeä olisi laittaa esimerkin henkilölle ala-asennossa 150 kg tankoon?

Silloin antamasi esimerkit ovat samanlaiset. Väitätkö siis että antamasi esimerkin mukaan on eroa tuottaa voimaa tangon ollessa ylä asennossa vs ala asennossa? Kuorma on edelleen joko se 100kg tai 150kg. Eli esimerkissäsi toisessa kyetään konsentrisen voimantuoton kautta liikuttamaan painoa ylös päin. Toisessa esimerkin painolla 150kg sama määrä konsentrista voimaa ei riitä edes kuorman pysäyttämiseen.

Eksentrissä vaiheessa on mahdollista tuottaa enemmän voimaa, kuin konsentrisessa.

No nyt!! Nimenomaan on mahdollista!!!!! Ei mikään sääntö!!! Ja nimen omaan eksentrisessä vaiheessa ei voimaa!!! No nyt lue esim tuosta kirjasta linkatut sivut. Ellet ole niitä jo lukenut.

Ja vielä selvennyksenä, jos 100 kg penkkipunnertaja laskee 100 kg rinnalle ja nostaa sen jälkeen ylös, tässä suorituksessa konsentrisen vaiheen voimantuotto oli suurempaa, kuin eksentrisen.

Kyllä eli eksentrisessä suunnassa tuotettiin vähemmän voimaa.

Nostajalla olisi tietysti mahdollisuus tuottaa eksentrisessä vaiheessa enemmän voimaa, jolloin tangon liike hidastuu ja vaikka pysähtyy kesken laskun.

Joka on kuitenkin vähemmän mitä konsentriseen suuntaan liikkuminen vaatisi eikö?

 

[En kerro!!!]

Ei se mikään sääntö ole koskaan ollutkaan, että eksentrisessä vaiheessa tuotetaan enemmän voimaa. Ihminen kykenee säätämään voimantuottoaan. Kyse on vain siitä, että eksentrisessä vaiheessa on MAHDOLLISTA tuottaa enemmän voimaa, kuin konsentrisessa.

Jos 100 kg penkkipunnertaja kykenee kontrolloimaan mitenkään 150 kiloa, tai edes 120 kiloa negatiivisessa toistossa, tarkoittaa se sitä, että eksentrisen vaiheen voimantuotto on suurempaa. Piste.