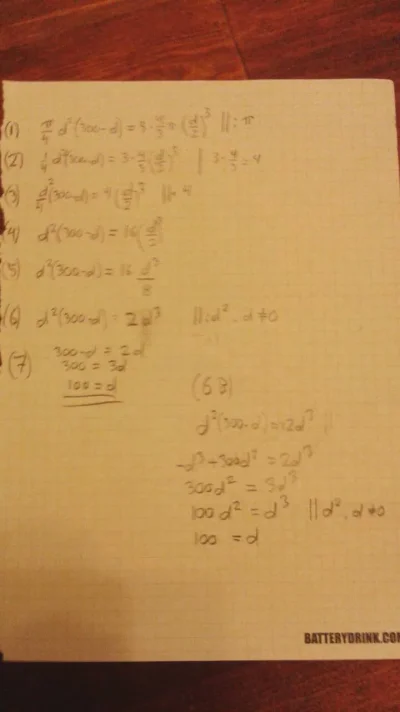Matemaattinen ongelma tai jotain

  • Keskustelun aloittaja Keskustelun aloittaja Nor
  • Aloitettu Aloitettu
Harjoitellut tuleviin AMK:n tekniikan ja liikenteen alan valintakokeisiin ja viime kevään tehtävistä löytyy yksi yhtälö, jota en vain saa menemään. Tästä linkistä pääsee vastauksiin, jossa kyseinen yhtälö on muodostettu ja pyöristetty vastauskin annettu. Matematiikan osiossa siis kysymys numero 3. En tosin usko, että monikaan amispohjainen tuon handlaa muutenkaan, mutta tuo tehtävä vaivaa mieltä.
 
Ton säiliön tilavuus on lieriöosan tilavuus plus pallon tilavuus. (puolipallo molemmissa päissä). Halutaan että koko säiliön tilavuus on nelinkertainen palloon nähden joten lieriöosan tilavuus = 3x pallon tilavuus. (kok. tilavuus silloin 3x pallo+2x0.5 palloa puolipalloista)

Loppuyhtälö on lieriöosan tilavuus eli pohjan ala PII×halkaisija toiseen/4 x pituus eli 300-d (puoli deetä molemmista päistä)

on yhtä suuri kuin 3 x pallon tilavuus.

sori sekava viesti, puhelimella :)
 
Kiitos avusta, ei vaan uppoa tähän päähän tuo. Jos riittää viitseliäisyyttä jollakulla niin olisi kiva nähdä miten tuo yhtälö ratkaistaan ihan vaihe vaiheelta. Mieluusti juurikin tuo yhtälö, joka on esimerkkinä tuolla vastaus-sivulla. Amiksestakin on jo muutama vuosi ja nyt lomautettuna on ollut aikaa kerrata näitä. Lienee tosiaan selvää, ettei tuollaista kauheasti ammattikoulussa tehty, mutta nyt oikeasti asiaan motivoituneena ärsyttää, kun ei viikkojen miettimisen aikana ole tuosta saanut tuota yhtälöä ratkotuksi. Lähinnä kiinnostaa missä kohtaa teen väärin, vastauksena kuitenkin tulee jotain suhteellisen järkevää eli ei tässä ihan hakoteillä olla :)
 
uploadfromtaptalk1394467918225.webp

1) Jaetaan pii pois molemmilta puolilta
2) sievennetään 3*4/3 =4
3) kerrotaan molemmat puolet neljällä niin päästään eroon vasemman puolen nelosesta
4)tässä ollaan nyt
5)kerrotaan auki (d/2)^3 = d^3 / 2^3 = d^3 / 8
6a) nyt voi joko jakaa molemmat puolet d^2, oletetaan että d ei ole nolla koska kyse on säilin halkaisijasta
6b) vaihtoehtoisesti ton voi kertoa auki ja jakaa myöhemmin sitten samalla tapaa d^2 :lla

7) lopuksi saadaan d=100

Enempää ei heru nyt. :)
 
Ihme kun ketään ei tullu nillittää detaljeista. Tuhannen taalan paikka.
 
Kun sekoitetaan 3litraa suolaliuosta A ja 4 litraa suolaliuosta B, saadaan fysikaalista suolaliuosta, jonka suolapitoisuus on 0,9%. Jos sekoitetaan 5 litraa liuosta A ja 2 litraa liuosta B, saadaan liuos jonka suolapitoisuus on 0,7%. Määritä liuosten A ja B suolapitoisuudet.

Sen verran ymmärsin että pitää yhtälöparina ratkaista. Onko yhtälöt sitten tällaiset: 3A+4B=0,9 ja 5A+2B=0,7? Vastaukseksi pitäisi tulla 0,5% ja 1,2%, mutta en noilla yhtälöillä sellaisia saa. Apuja kiitos!
 
Suolapitoisuushan on suolan määrä / kokonaistilavuus

(3A+4B) / 7 =0.009

(5A+2B)/ 7 = 0.007

3a+4b = 0.063
5a+2b= 0.049
--------------
kerro alempi kahdella ja vähennä yhtälöt toisistaan

7a= 0.035
a= 0.005
 
Nyt menee sormi suuhun taas yhtälöiden kanssa. Eli, jos yhtälössä on useampi muuttuja, kuten tässä C-kohdassa. Olen koittanut googletella "kahden muuttujan yhtälö" ja se ohjaa minut yhtälöpareihin, joka tässä ei kuitenkaan ole kyseessä? Haluaisin vaikka vaihe vaiheelta tämän laskettuna tai jotain linkkiä, jossa asia selitetään.
 
Tollaisessa tapauksessa sä ratkaiset muuttujan x A:n suhteen eli se on yleinen ratkaisu ja A:n paikalle voisi sitten sijoittaa mitä haluaa. Jos nyt nopeasti katoin päässä oikein niin tuosta pitäisi tulla x = 3A/(1-A).
 
Eli vähän matematiikkaa ja Excelin käyttöä. Mulla ihan kokeellisesti havaittu ilmiö josta on väännetty jonkinlainen kuvaaja. Eli tiedetään arvot x- ja y-akseleilta (arvot 1 ja 2), sitten siivutetaan tuonne oikeaan y-akseliin ja saadaan arvo 3. Mitkään noi arvot ei oo toisten kanssa korrelaatiossa vaan ihan kokeilemalla saatuja juttuja ja haluaisin siirtää tuon sellaiseen muotoon exceliin että kun syöttää arvot 1 ja 2 niin saadaan arvo 3. Eli lähtökohtana olisi varmaan suoran yhtälön muodostus ja kun noilla suorilla ei oo eroa kuin tuo y-akselin leikkauspiste. Sitten muodostetaan tuolle toiselle y-akselille suoran yhtälö ja lasketaan noiden suorien leikkauspiste. Kuinkas sitten tuosta leikkauspisteen arvosta muodostetaan toi arvo 3 kun ei ole samalla skaalalla muiden akselien kanssa? Tuskin kukaan tajus mitään.
testi – Kopio.webp
 
Taipuisko aineisto siihen että lasket suoraan tuon arvon? f (1, 2) -> 3. Se ois vaan yhden kaavan perustrigonometriaa.

Viivakikkailu varmasti onnistuu myöa mutta vaatinee paljon excelin ohjeen ja googlen konsultointia...
 
Oiskohan tuossa kyse siitä, että tekisit valmiin taulukon arvoilla 1 ja 2, niistä teet tuon käyrästön, siihen trendikäyrä, ja katsot trendikäyrän laskentakaavan (exceli ilmoittaa myös trendikäyrän pätevyysasteen), joka sitten laskee arvon 3? Tuo arvo 3 näyttäisi olevan lineaarinen piirroksestasi katsottuna, x ja y arvoista en sitten tiedä, mutta excel osaa sovittaa melko hankaliakin kaavoja ns. satunnaisille pistejonoille, mikäli niiden leikkauspiste kekkuloi esitetyllä alueella mielivaltaisesti. Y-akseleitahan tuossa on 1 kpl, tuolla oikealla reunassa olevan pisteen arvo vaan on tuosta piirustuksesta katsottuna Y:n arvo 1 + jotain.

Enempää en tuosta nyt kyllä tajunnut, mutta jos tuo arvo 3 tulee lineaarisesti X-ja Y akselien leikkauspisteestä, niin olisiko ylläolevasta apuja..
 
Osaisiko joku auttaa tässä?

Rakennus, jonka päädyn leveys on 6,0 metriä, katetaan harjakatolla, jonka lappeiden leveys (eli katon pituus harjalta molempiin harjakaton alareunoihin) on 5,0 metriä. Kuinka suuri katon kaltevuuskulman tulee olla, jotta katto ulottuu mahdollisimman alas (matalalle)?

Ratkaisussamme merkataan d=sivu joka tulee täydentäessä seinän yli menevästä katon osasta ja seinästä suorakulmainen kolmio. X on kaltevuuskulma radiaaneina.
Sitten lyödään suoraan pöytään funktio d=f(x)=sin(x)(5-(3/cos(x)))

kysymys kuuluukin mistä tämä funktio saadaan? ja siis tuo sin(x) jälkeinen sulkuhirviö on 5-murtoluku jossa ylhäällä 3 alhaalla cos(x).
 
Tovi sanoi:
kysymys kuuluukin mistä tämä funktio saadaan?
Click to expand...

katon harjan osasta ja talon leveyden puolikkaan muodostamasta suorakulmasesta kolmiosta saadaan:
cos(x)=3/a, missä a on katon osa joka ei mene yli seinästä.
=> a=3/cos(x)

seinän yli menevästä katon harjasta ja seinästä muodostuvasta suorakulmasesta kolmiosta saadaan:
Jos d tosiaan on tuo täydentävä sivu, niin
cos(x)=d/(5-a)
=>d=cos(x)*(5-a)
eli d=cos(x)*(5-3/cos(x))

Epäilen kyllä vahvasti, että d kirjaimella on tuossa sinun ratkasussa merkitty kolmion sivua, joka on talon seinän suuntainen. Koska silloin tulis tuo sinun versio:
d=sin(x)*(5-3/cos(x))

Tuon suurin arvo näyttää tulevan, kun katon kaltevuuskulma on asteina n.32,5.
 
Kiitos paljon, nyt selveni! Ja joo omat sanat menivät sekaisin kun koitin saada tuon ymmärrettävään muotoin ilman mallikuvaa. d oli siis seinän suuntainen sivu tuossa kolmiossa :)
 
Miten lasketaan vaakasuoralla pinnalla vedettävän kappaleen liikekitkakerroin jos on annettu kappaleen massa (15kg), vetävä voima (50N) ja kiihtyvyys 0,75m/s^2?
 
Back
Ylös Bottom