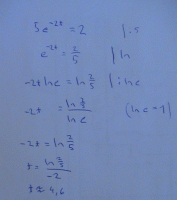Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Huomio: This feature may not be available in some browsers.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Apua (typerä matikkapulma)
- Keskustelun aloittaja kgb
- Aloitettu
- Status
- Viestiketju on suljettu.
Lisää vaihtoehtoja
Meta tags- Liittynyt
- 16.12.2002
- Viestejä
- 250
Re: Apua
Ehkävastaus
t=(ln 2/5)/-2
likiarvo = 0,458
Originally posted by kgb
Ratkaise t.
5*e^-2t =2
Ehkävastaus
t=(ln 2/5)/-2
likiarvo = 0,458
Viikate74
Bukkake Fighter
- Liittynyt
- 22.2.2003
- Viestejä
- 1 788
Re: Apua
Istutko kokeessa :thumbs:
Originally posted by kgb
Voisiko joku viisas kertoa miten nuo ratkaistaan.
Ratkaise t.
5*e^-2t =2
Ratkaise k.
N=Noe^kt
Kiitoksia etukäteen.
Istutko kokeessa :thumbs:
- Liittynyt
- 1.4.2003
- Viestejä
- 434
Re: Re: Apua
Noin mäkin sitä ratkaisin, mutta en tiedä onko oikein.
Originally posted by Huonojalkainen
Ehkävastaus
t=(ln 2/5)/-2
likiarvo = 0,458
Noin mäkin sitä ratkaisin, mutta en tiedä onko oikein.
- Liittynyt
- 9.11.2002
- Viestejä
- 270
- Liittynyt
- 18.4.2002
- Viestejä
- 1 779
Re: Apua
1.
5*e^(-2t)=2
e^(-2t)=2/5 | ln
ln e^(-2t)=ln 2/5
-2t =ln 2/5
t =-1/2ln 2/5
t =ln SQR(5/2)
2.
N=Noe^kt
e^kt=N/No
ln e^kt=ln N/No
kt=ln N/No
k= ln (N/No)^(1/t)
Originally posted by kgb
Ratkaise t.
5*e^-2t =2
Ratkaise k.
N=Noe^kt
1.
5*e^(-2t)=2
e^(-2t)=2/5 | ln
ln e^(-2t)=ln 2/5
-2t =ln 2/5
t =-1/2ln 2/5
t =ln SQR(5/2)
2.
N=Noe^kt
e^kt=N/No
ln e^kt=ln N/No
kt=ln N/No
k= ln (N/No)^(1/t)
- Status
- Viestiketju on suljettu.