- Liittynyt
- 9.5.2004
- Viestejä
- 632
Kaveri linkitti netistä tällasen aika kummallisen kuvan.
http://www.ebaumsworld.com/2006/08/trigrid.gif
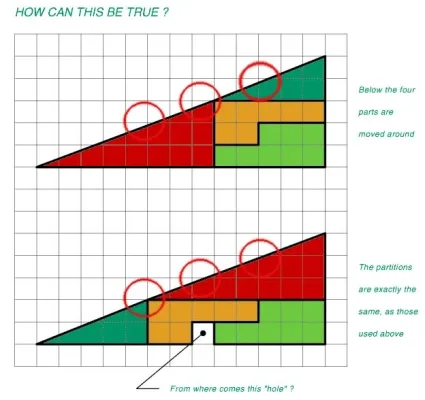
Kukaan kenelle oon ton näyttäny, ei oo tajunnu, että miten toi on mahdollista. Oon ite laskenu, että ylemmän kolmion pinta-ala on 32,5 ja alemman tietenki 31,5 , mutta sen lisäks ihmetyttää se, että kun lasken kaikkien osien pinta-alat erikseen ja plussaan yhteen, niistä tulee 32??
Osaako joku fiksu selittää tän?
http://www.ebaumsworld.com/2006/08/trigrid.gif
Kukaan kenelle oon ton näyttäny, ei oo tajunnu, että miten toi on mahdollista. Oon ite laskenu, että ylemmän kolmion pinta-ala on 32,5 ja alemman tietenki 31,5 , mutta sen lisäks ihmetyttää se, että kun lasken kaikkien osien pinta-alat erikseen ja plussaan yhteen, niistä tulee 32??
Osaako joku fiksu selittää tän?